Finding possible permutations of an array

As every person once in life needs to find all possible permutations of an array, this day I had this moment. I saw it in a YT video as an interview question and i thought its a cool question and tried to solve it. And it took longer than expected but at the end we have a working solution. In this article I will just share the code and try to go over the first several steps explaining in text. With recursion I always have to write it down on a paper otherwise my brain will not get it.

The solution:

#include <string>
#include <iostream>
#include <vector>
#include <algorithm>

// Example of DFS ( Depth first search )
void permuteMe( std::vector<std::vector<int32_t> >& ans, std::vector<int32_t>& sol, std::vector<int32_t>& arr )
{
   std::cout << ">>>> Entering permute\n";
   std::cout << "[ ";
   for( auto n : sol )
   {
      std::cout << n << " ";
   }
   std::cout << "]\n";

   if( sol.size() == arr.size() )
   {
      ans.push_back( sol );
      std::cout << ">>>> Exiting permute size reached\n";
      return;
   }

   for( auto num : arr )
   {
      std::cout << "Next Number: " << num << "\n";
      // The next number is already part of the partial solution
      if( std::find( sol.begin(), sol.end(), num ) != sol.end() )
      {
         continue;
      }

      sol.push_back( num );
      permuteMe( ans, sol, arr );
      std::cout << "Popping: " << sol.back() << "\n";
      sol.pop_back(); // Important step to be able to go back the tree
   }
   std::cout << ">>>> Exiting permute\n";
}

int main()
{
   // Permutation sind n!
   // 9! = 362,880 moegliche permutationen
   std::vector<int32_t> arr = {1,2,3};

   std::vector<std::vector<int32_t> > ans;
   std::vector<int32_t> sol;

   permuteMe( ans, sol, arr );

   for( auto solArr : ans )
   {
      std::cout << "[ ";
      for( auto n : solArr )
      {
         std::cout << n << " ";
      }
      std::cout << "]\n";
   }

   return 0;
}

Ignore the cout calls :)

So the possible permutations for this question is n! in which n is the number of elements in the array.

Step by Step

Enough of talk we have the code and now we run the program in our head:

Recursion Level: X indicates at which level we currently are.

Recursion Level: 0
- Entering permuteMe
- Entering the for loop in permuteMe starting with the first number 1
- Pushing 1 to the solution array -> Solution array [1]
- Calling permuteMe
- Currently we are at the number 1 in the for loop
Recursion Level: 1
- Entering permuteMe
- Entering the for loop
  - We skip the first iteration (number 1) because it is already added to the solution array. Following code is skipping numbers which are part of the solution already
```
if( std::find( sol.begin(), sol.end(), num ) != sol.end() )
{
    continue;
}
```
- Next iteration with number 2
- We add the number 2 to the solution array -> [1,2]
- Calling permuteMe
- Currently we are at the number 2 in the loop
Recursion Level: 2
- Entering permuteMe
- Entering the for loop
  - We skip the first two numbers because they are already part of the solution array
- Next iteration with number 3
- Pushing number 3 to the solution array -> [1,2,3]
- Calling permuteMe
- Currently we are at the number 3 in the loop
Recursion Level: 3
- Entering permuteMe
- Now we entering this if clausel which indicates we reached a leaf node and there are no possible permutations left on this path. We are pushing this partial soluation (sol vector) into the ans vector which holds all the possible permutations.
```
if( sol.size() == arr.size() )
{
    ans.push_back( sol );
    std::cout << ">>>> Exiting permute size reached\n";
    return;
}
```
As we can see in the code above we are returning from this function so we are exiting this recursion level and will continue from Recursion Level 2
- Returning from Recursion Level: 3
Entering Recursion Level: 2 ( Basically continue from Step 3 )
- Returning from permuteMe
- Popping the last element from sol array which is 3. Befor: [1,2,3] -> After: [1,2]
- We are currently still at number 3 check Point 3
- This means we are exiting the loop and returning from this recursion level
- Returning from Recursion Level: 2
Entering Recursion Level: 1 ( Basically continue from Step 2 )
- Popping the last element from sol array which is 2. Befor: [1,2] -> [1]
- We are currently still at the number 2 in this Recursion level
- Because we popped the last element the next instruction is to go to the next iteration which is 3
- Pushing number 3 to the sol array -> [1,3]
- Calling permuteMe
- Currently we are at the number 3 in the loop
Entering Recursion Level: 2
- Skipping Number 1
- Pushing 2 to the solution array -> [1,3,2]
- Calling permuteMe
- Currently we are at the number 2 in the loop
Recursion Level: 3
- Entering permuteMe
- Now we entering this if clausel which indicates we reached a leaf node and there are no possible permutations left on this path. We are pushing this partial soluation (sol vector) into the ans vector which holds all the possible permutations.
```
if( sol.size() == arr.size() )
{
    ans.push_back( sol );
    std::cout << ">>>> Exiting permute size reached\n";
    return;
}
```
As we can see in the code above we are returning from this function so we are exiting this recursion level and will continue from Recursion Level 2
- Returning from Recursion Level: 3
Entering Recursion Level: 2 ( Basically continue from Step 7 )
- Popping the last number Befor: [1,3,2] --> After: [1,3]
- Because we are still at number 2 in this iteration we continue with the next iteration
- Next iteration with Number 3
- We skip the next iteration (number 3) because it is already added to the solution array. Following code is skipping numbers which are part of the solution already
```
if( std::find( sol.begin(), sol.end(), num ) != sol.end() )
{
    continue;
}
```
- Returning from Recursion level: 2
Entering Recursion level: 1 ( basically continue from step 6 )
- Popping last added element Befor: [1,3] --> After: [1]
- We try to iterate over the next element which does not exist because we are at the last element already (check step 6 iteration)
- Returning from Recursion level: 1
Entering Recursion level: 0 ( basically continue from step 1 )
- Popping last element in solution Befor: [1] --> After: [ ]
- Entering next iteration which is number 2
- Pushing number 2 to the solution array
- Calling permuteMe

Basically thats it after that it is only repeating. In the steps above we finished following tree branch:

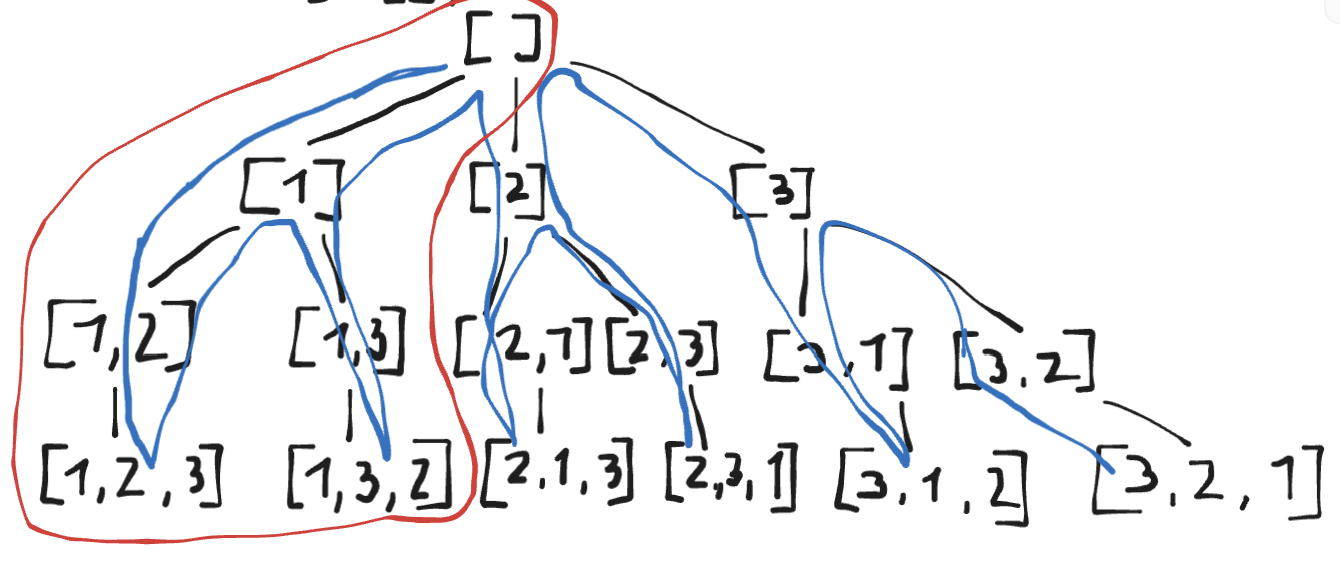
The red "circle" shows our path which we solved by hand step by step